稀疏张量网络¶
稀疏张量¶
在传统的语音、文本或图像数据中,特征是被密集提取的。因此,用于这些数据的最常见的表示形式是向量、矩阵和张量。但是,对于三维扫描甚至更高维度的空间,这种密集表示效率低下,因为有效信息仅占据空间的一小部分。相反,我们可以只保存空间非空区域的信息,类似于我们如何保存稀疏矩阵上的信息。这种表示是稀疏矩阵的 N 维扩展;因此,它被称为稀疏张量。
在 Minkowski Engine 中,我们采用稀疏张量作为基本数据表示,该类提供为 MinkowskiEngine.SparseTensor。有关稀疏张量的更多信息,请参阅术语页面。
稀疏张量网络¶
压缩神经网络以加速推理并最大限度地减少内存占用已被广泛研究。模型压缩的流行技术之一是修剪卷积网络中的权重,也称为稀疏卷积网络 [1]。这种用于模型压缩的参数空间稀疏性仍然在密集张量上运行,并且所有中间激活也是密集张量。
但是,在这项工作中,我们关注的是空间稀疏数据,特别是空间稀疏高维输入和用于稀疏张量的卷积网络[2]。我们也可以将这些数据表示为稀疏张量,并且在高维问题(如 3D 感知、配准和统计数据)中很常见。我们将专门针对这些输入的神经网络定义为稀疏张量网络,这些稀疏张量网络处理并生成稀疏张量[4]。为了构建稀疏张量网络,我们构建所有标准神经网络层,例如 MLP、非线性、卷积、归一化、池化操作,就像我们在密集张量上定义并在 Minkowski Engine 中实现的方式一样。
广义卷积¶
卷积是许多领域中的基本操作。在图像感知中,卷积一直是许多任务中实现最先进性能的关键,并且被证明是 AI 和计算机视觉研究中最关键的操作。在这项工作中,我们采用稀疏张量上的卷积 [2] 并提出了稀疏张量上的广义卷积。广义卷积将所有离散卷积作为特殊情况包含在内。我们不仅在 3D 空间轴上使用广义卷积,而且在任何任意维度上,或者在时间轴上使用广义卷积,这已被证明在某些应用中比循环神经网络 (RNN) 更有效。
具体来说,我们概括了通用输入和输出坐标的卷积,以及任意内核形状的卷积。它允许将稀疏张量网络扩展到极高维空间,并动态生成生成任务的坐标。此外,广义卷积不仅包含所有稀疏卷积,还包含传统的密集卷积。我们列出了下面广义卷积的一些特性和应用。
令 \(x^{\text{in}}_\mathbf{u} \in \mathbb{R}^{N^\text{in}}\) 为 \(N^\text{in}\) 维输入特征向量,位于 \(D\) 维空间中的 \(\mathbf{u} \in \mathbb{R}^D\) 处(D 维坐标),卷积核权重为 \(\mathbf{W} \in \mathbb{R}^{K^D \times N^\text{out} \times N^\text{in}}\)。我们将权重分解为具有大小为 \(N^\text{out} \times N^\text{in}\) 的 \(K^D\) 个矩阵的空间权重,表示为 \(W_\mathbf{i}\),其中 \(|\{\mathbf{i}\}_\mathbf{i}| = K^D\)。那么,D 维中的传统密集卷积是
其中 \(\mathcal{V}^D(K)\) 是以原点为中心的 \(D\) 维超立方体中的偏移列表。例如,\(\mathcal{V}^1(3)=\{-1, 0, 1\}\)。以下等式中的广义卷积放宽了上述等式。
其中 \(\mathcal{N}^D\) 是一组定义内核形状的偏移量,\(\mathcal{N}^D(\mathbf{u}, \mathcal{C}^\text{in})= \{\mathbf{i} | \mathbf{u} + \mathbf{i} \in \mathcal{C}^\text{in}, \mathbf{i} \in \mathcal{N}^D \}\) 是来自当前中心 \(\mathbf{u}\) 的偏移量集,该偏移量存在于 \(\mathcal{C}^\text{in}\) 中。\(\mathcal{C}^\text{in}\) 和 \(\mathcal{C}^\text{out}\) 是稀疏张量的预定义输入和输出坐标。首先,请注意,输入坐标和输出坐标不一定相同。其次,我们使用 \(\mathcal{N}^D\) 任意定义卷积核的形状。这种概括包含许多特殊情况,例如扩张卷积和典型的超立方体内核。另一个有趣的特殊情况是稀疏子流形卷积,当我们设置 \(\mathcal{C}^\text{out} = \mathcal{C}^\text{in}\) 且 \(\mathcal{N}^D = \mathcal{V}^D(K)\) 时。如果我们设置 \(\mathcal{C}^\text{in} = \mathcal{C}^\text{out} = \mathbb{Z}^D\) 且 \(\mathcal{N}^D = \mathcal{V}^D(K)\),则稀疏张量上的广义卷积将变为传统的密集卷积。如果我们定义 \(\mathcal{C}^\text{in}\) 和 \(\mathcal{C}^\text{out}\) 作为自然数的倍数,并且 \(\mathcal{N}^D = \mathcal{V}^D(K)\),我们有一个跨步密集卷积。
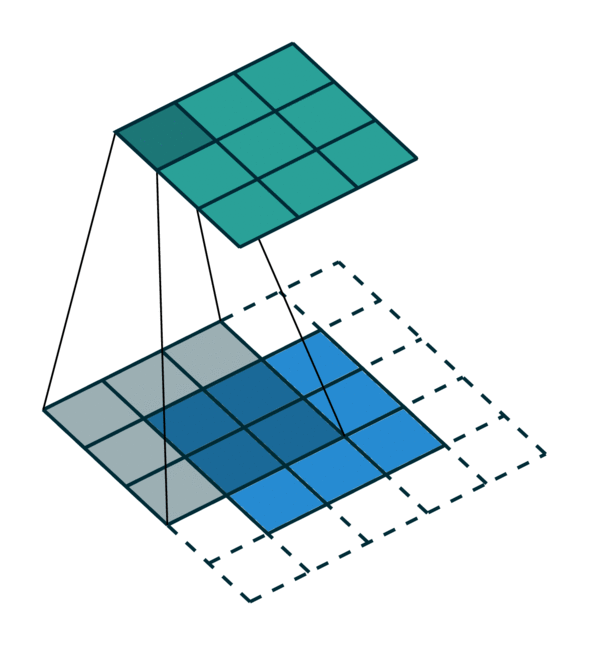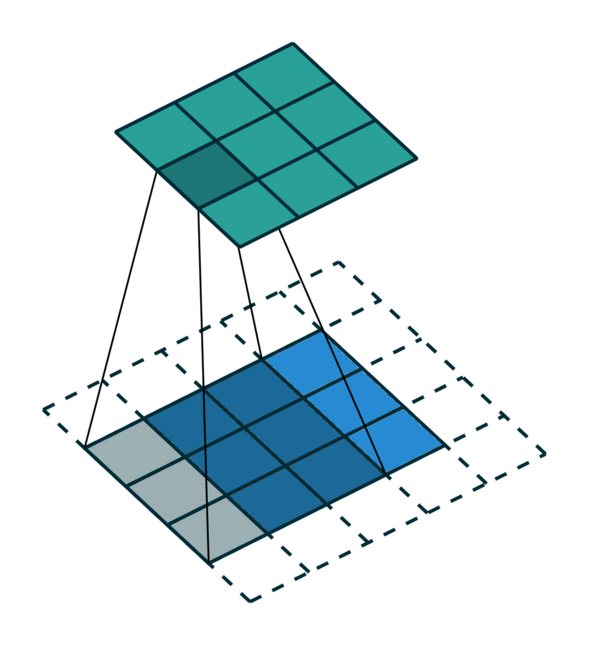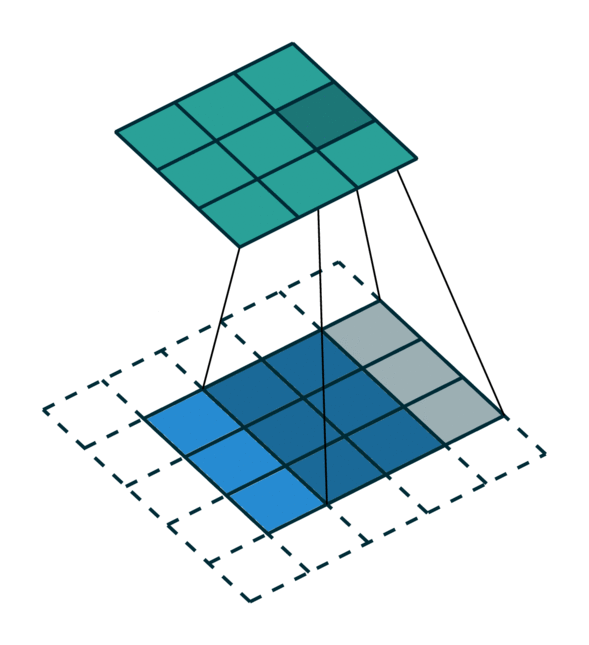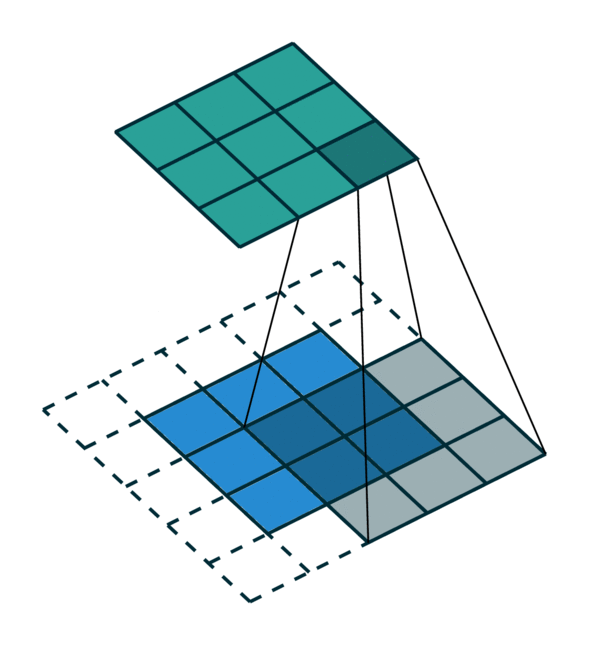
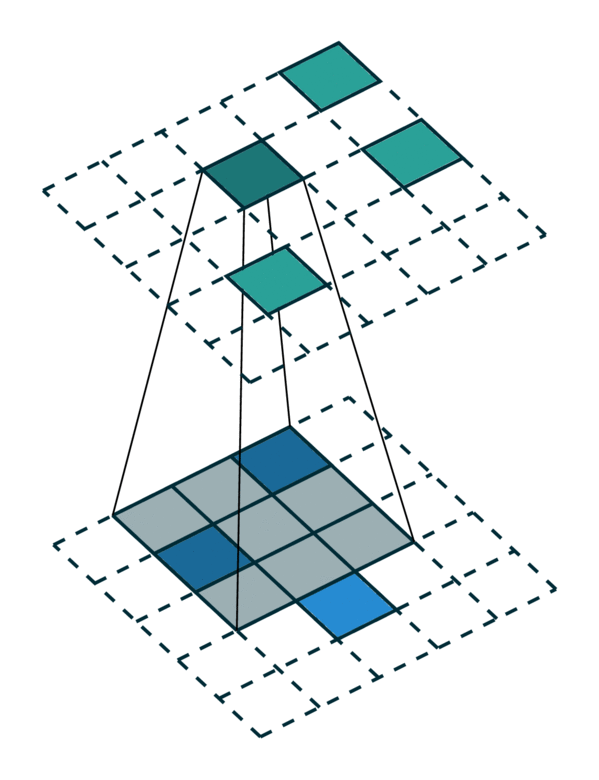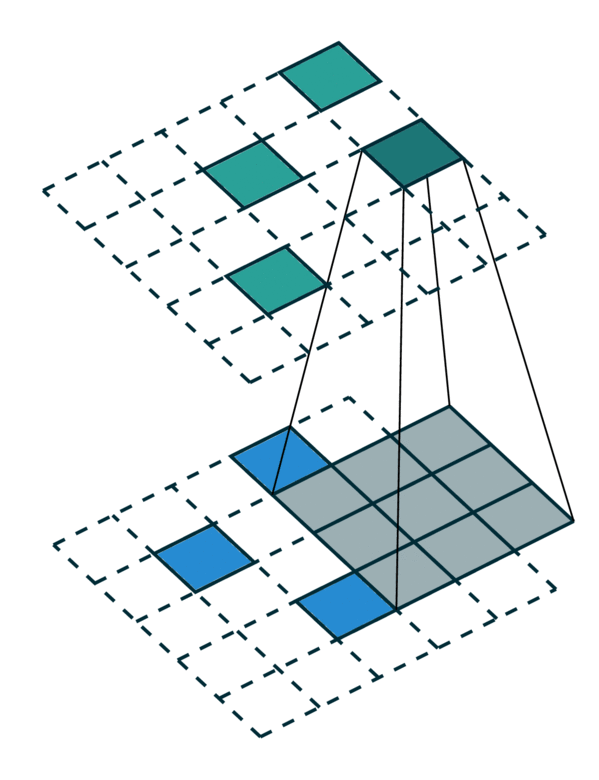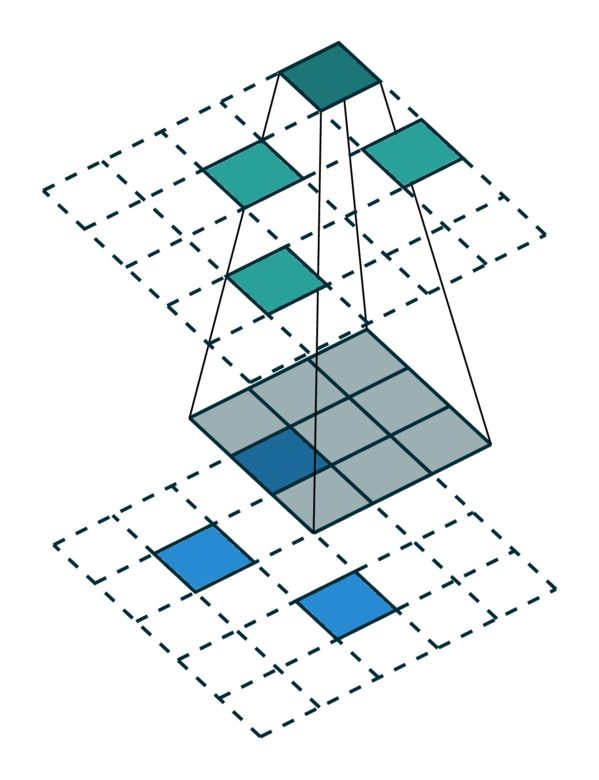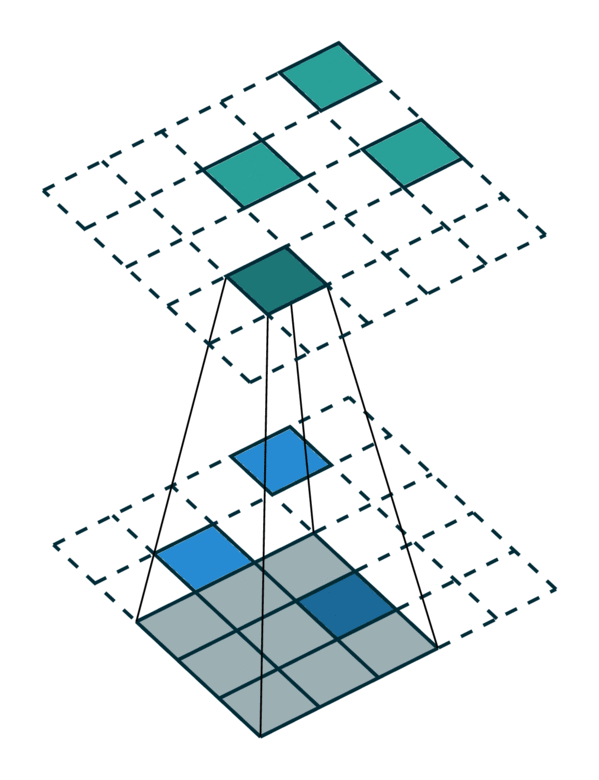
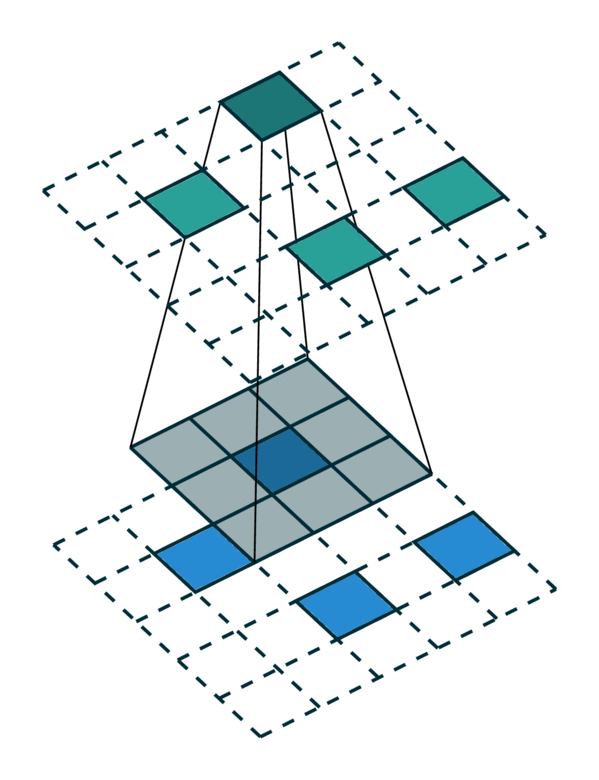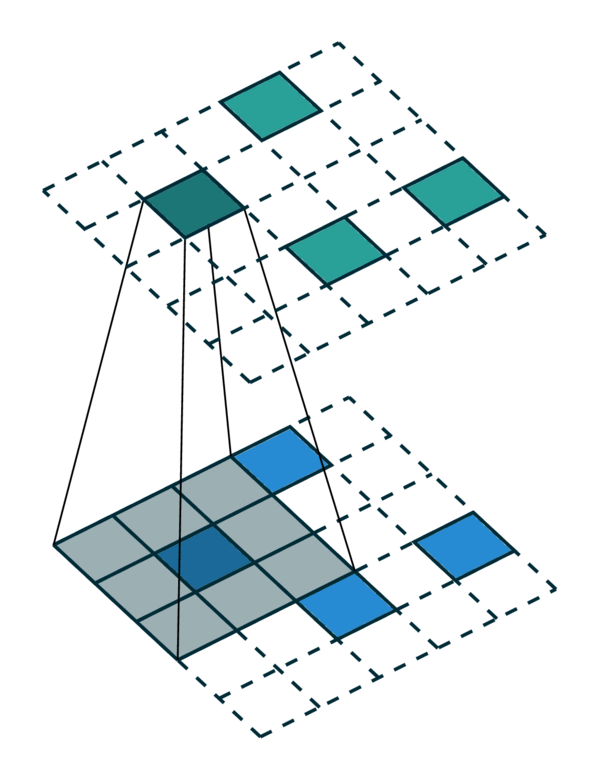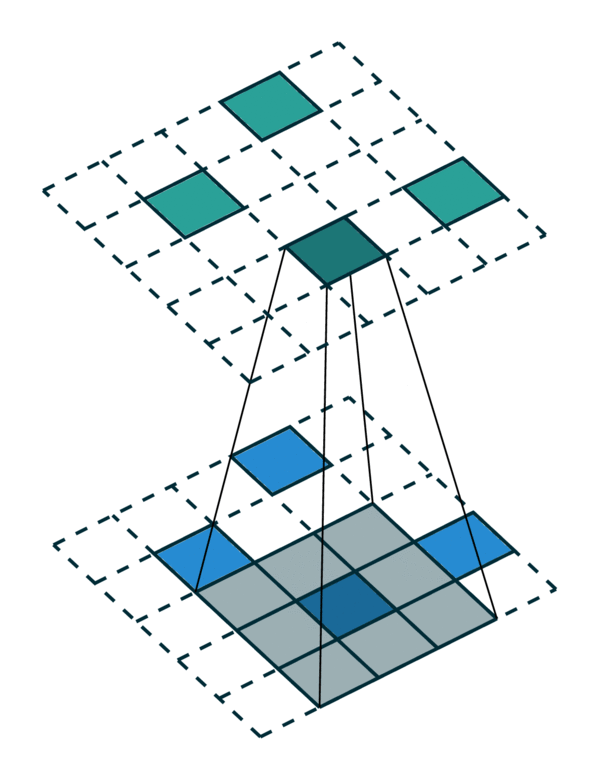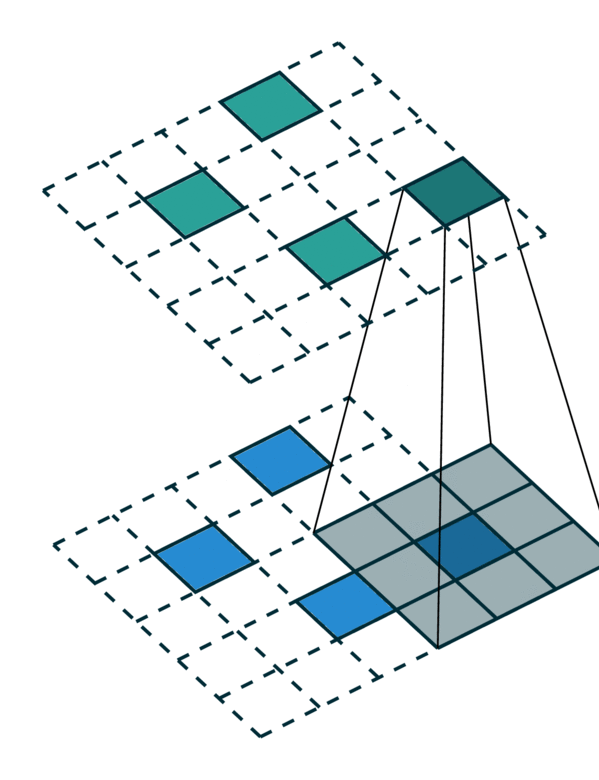
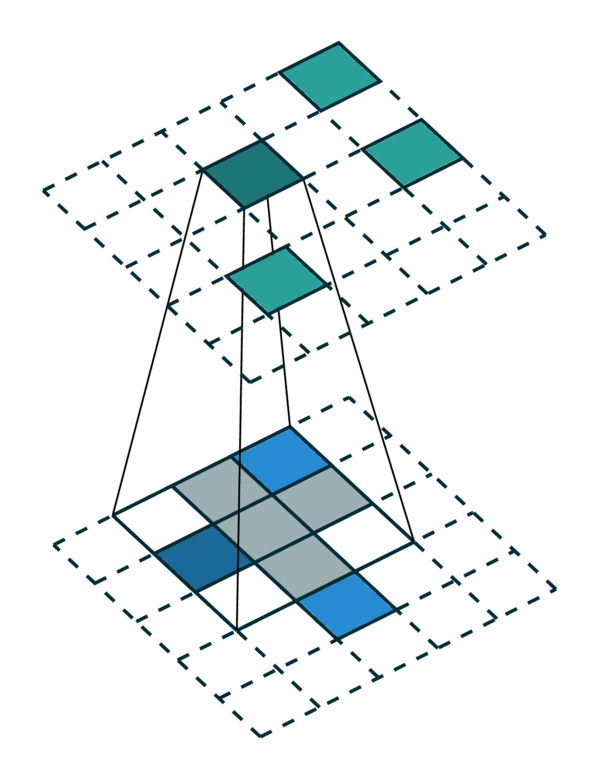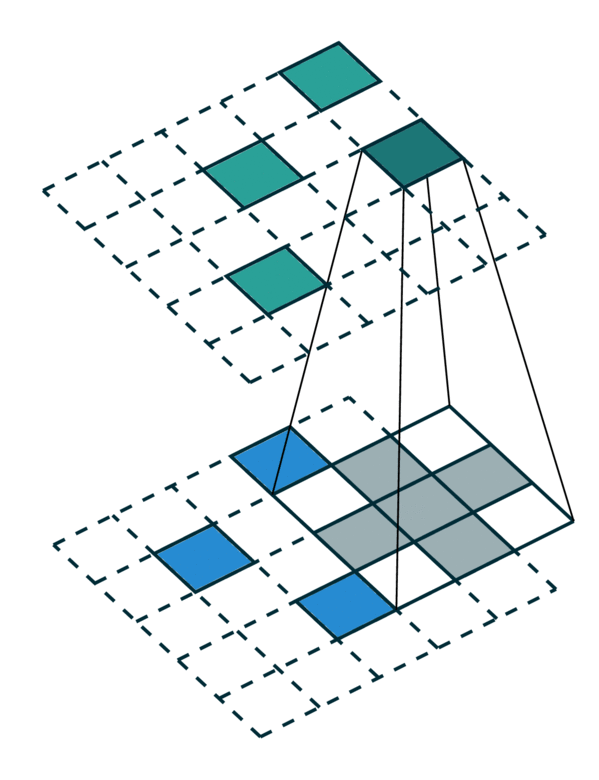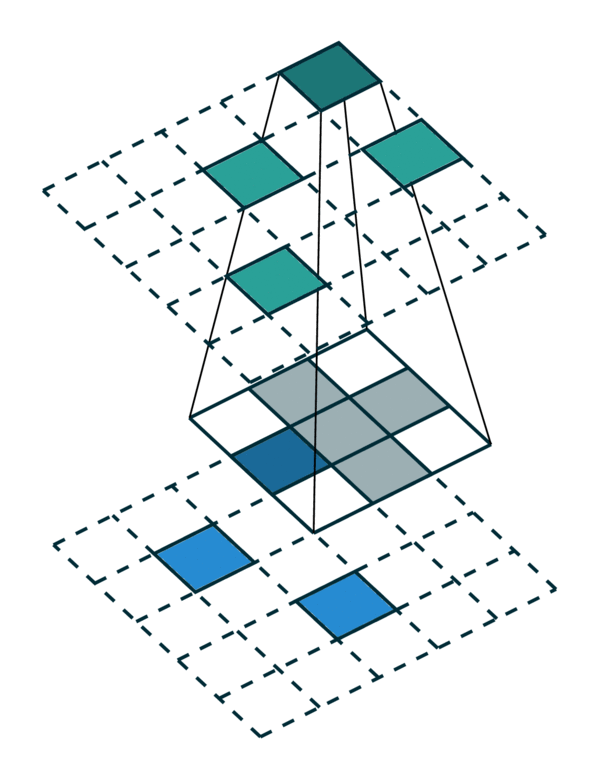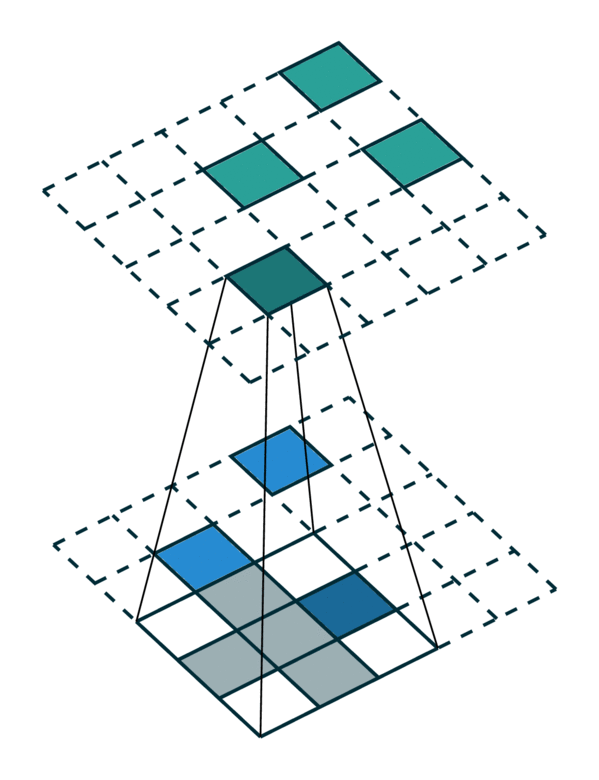
我们可视化了在密集张量和稀疏张量上进行简单 2D 图像卷积。请注意,稀疏张量上的卷积顺序不是顺序的。
密集张量 |
稀疏张量 |
|---|---|
[照片来源:Chris Choy] |
|
为了有效地计算稀疏张量上的卷积,我们必须找到输入稀疏张量中的每个非零元素如何映射到输出稀疏张量。我们将此映射称为内核映射 [3],因为它定义了如何通过内核将输入映射到输出。有关更多详细信息,请参阅术语页面。
广义卷积的特殊情况¶
广义卷积包含了所有离散卷积作为其特殊情况。我们将在本节中介绍几个特殊情况。首先,当输入和输出坐标都是网格上的所有元素时,即密集张量,则广义卷积等效于密集张量上的规则卷积。其次,当输入和输出坐标是稀疏张量上非零元素的坐标时,则广义卷积变为稀疏卷积 [2]。此外,当我们使用超十字形内核 [3] 时,广义卷积等效于可分离卷积。
相同的输入/输出坐标 |
任意的输入/输出坐标 |
广义卷积 |
|---|---|---|
[照片来源:Chris Choy] |
||