定义和术语

稀疏张量

稀疏张量是稀疏矩阵的高维扩展，其中非零元素表示为一组索引 \(\mathcal{C}\) 和关联值（或特征） \(\mathcal{F}\)。 我们使用 COOrdinate 列表 (COO) 格式来保存稀疏张量 [1]。 这种表示形式只是将坐标连接成一个矩阵 \(C\) 和关联值或特征 \(F\)。 在传统的稀疏张量中，索引或坐标必须是非负整数，而在 Minkowski Engine 中，负坐标也是有效的坐标。 最终的稀疏张量 \(\mathscr{T}\) 具有 \(D\) 维坐标，如果特征是标量，则是 rank-\(D\) 张量，如果特征是向量，则是 rank-\(D + 1\)。

\[\begin{split}\mathbf{C} = \begin{bmatrix} x_1^1 & x_1^2 & \cdots & x_1^D \\ \vdots & \vdots & \ddots & \vdots \\ x_N^1 & x_N^2 & \cdots & x_N^D \end{bmatrix}, \; \mathbf{F} = \begin{bmatrix} \mathbf{f}_1^T\\ \vdots\\ \mathbf{f}_N^T \end{bmatrix}\end{split}\]
\[\begin{split}\mathscr{T}[x^1_i, x^2_i, \cdots, x^D_i] = \begin{cases} \mathbf{f}_i \;\; & \text{如果} \; (x^1_i, x^2_i, \cdots, x^D_i) \in \mathcal{C} \\ 0 \;\; & \text{否则} \end{cases}\end{split}\]

总之，稀疏张量由一组坐标 \(\mathcal{C}\) 或等效地由一个坐标矩阵 \(C \in \mathbb{Z}^{N \times D}\) 和关联特征 \(\mathcal{F}\) 或一个特征矩阵 \(F \in \mathbb{R}^{N \times N_F}\) 组成，其中 \(N\) 是稀疏张量中非零元素的数量， \(D\) 是空间的维度，而 \(N_F\) 是通道的数量。 稀疏张量中的其余元素为 0。

张量步长

神经元的感受野大小定义为神经元在一层中可以看到的输入图像中像素之间沿一个轴的最大距离。 例如，如果我们使用内核大小为 3 和步长为 2 的两个卷积层处理图像，则第一个卷积层之后的感受野大小为 3； 第二个卷积层之后的感受野大小为 7。这是因为第二个卷积层看到的是以因子 2 或步长 2 对图像进行子采样的特征图。 这里，步长是指神经元之间的距离。 第一个卷积之后的特征图的步长大小为 2，第二个卷积之后的特征图的步长大小为 4。 类似地，如果我们使用转置卷积（反卷积、上卷积），则减小步长。

我们将张量步长定义为上面示例中这些 2D 步长的高维对应物。 当我们使用步长大于 1 的池化层或卷积层时，输出特征图的张量步长会增加该层的步长因子。

坐标管理器

许多基本操作（例如卷积、池化等）都需要找到非零元素之间的邻居。 如果我们使用跨步卷积或池化层，则需要生成一组新的输出坐标，这些坐标与输入坐标不同。 所有这些与坐标相关的操作都由坐标管理器管理。 需要注意的是，坐标管理器会缓存所有坐标和核映射，因为这些坐标和核映射会被非常频繁地重复使用。 例如，在许多传统的神经网络中，我们会串联多次重复相同的操作，例如 ResNet 或 DenseNet 中的多个残差块。 因此，坐标管理器会缓存所有这些，并在检测到字典中相同的操作时重复使用，而不是重新计算相同的坐标和相同的核映射。

在 Minkowski Engine 中，我们在初始化 MinkowskiEngine.SparseTensor 时创建一个坐标管理器。 您可以选择通过在初始化期间提供可选的坐标管理器参数来与新的 MinkowskiEngine.SparseTensor 共享现有的坐标管理器。 您可以使用 MinkowskiEngine.SparseTensor.coords_man 访问稀疏张量的坐标管理器。

坐标键

在坐标管理器中，所有对象都使用无序映射进行缓存。 坐标键是用于缓存稀疏张量坐标的无序映射的哈希键。 如果两个稀疏张量具有相同的坐标管理器和相同的坐标键，则稀疏张量的坐标相同，并且它们共享相同的内存空间。

核映射

稀疏张量由一组坐标 \(C \in \mathbb{Z}^{N \times D}\) 和关联特征 \(F \in \mathbb{R}^{N \times N_F}\) 组成，其中 \(N\) 是稀疏张量中非零元素的数量， \(D\) 是空间的维度，而 \(N_F\) 是通道的数量。 为了找到如何使用空间局部操作（例如卷积或池化）将一个稀疏张量映射到另一个稀疏张量，我们需要找到输入稀疏张量中的哪个坐标映射到输出稀疏张量中的哪个坐标。

我们将这种从输入稀疏张量到输出稀疏张量的映射称为核映射。 例如，内核大小为 3 的 2D 卷积具有一个 \(3 \times 3\) 卷积内核，它由 9 个权重矩阵组成。 一些输入坐标使用每个内核映射到相应的输出坐标。 我们将映射表示为整数列表对：输入映射 \(\mathbf{I}\) 和输出映射 \(\mathbf{O}\)。 输入映射中的一个整数 \(i \in \mathbf{I}\) 指示输入稀疏张量的坐标矩阵或特征矩阵的行索引。 类似地，输出映射中的一个整数 \(o \in \mathbf{O}\) 也指示输出稀疏张量的坐标矩阵的行索引。 列表中的整数以输入映射中的第 k 个元素 \(i_k\) 对应于输出映射中的第 k 个元素 \(o_k\) 的方式排序。 总之，\((\mathbf{I} \rightarrow \mathbf{O})\) 定义了输入特征 \(F_I\) 的行索引如何映射到输出特征 \(F_O\) 的行索引。

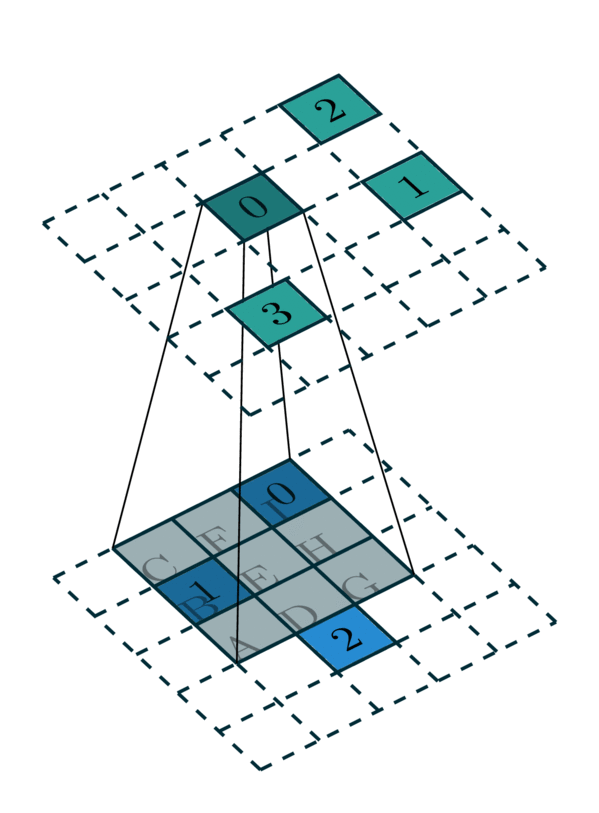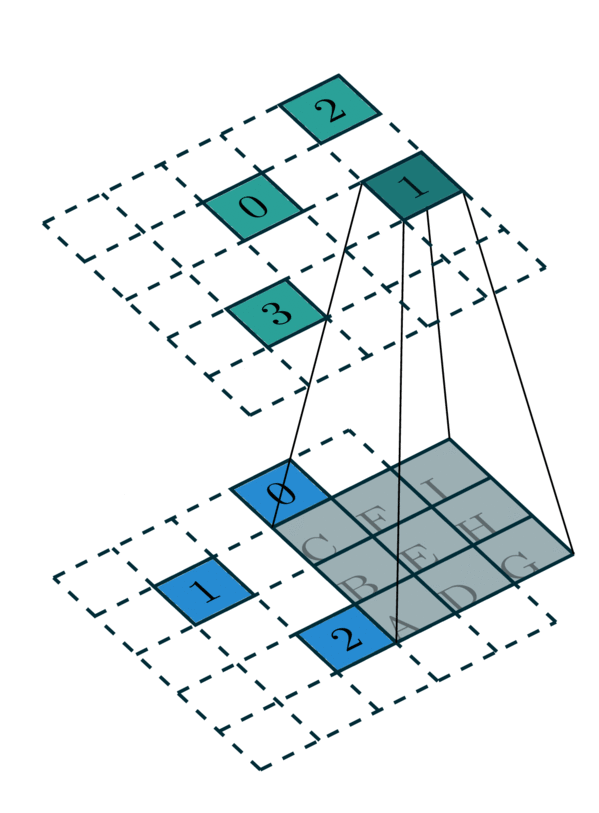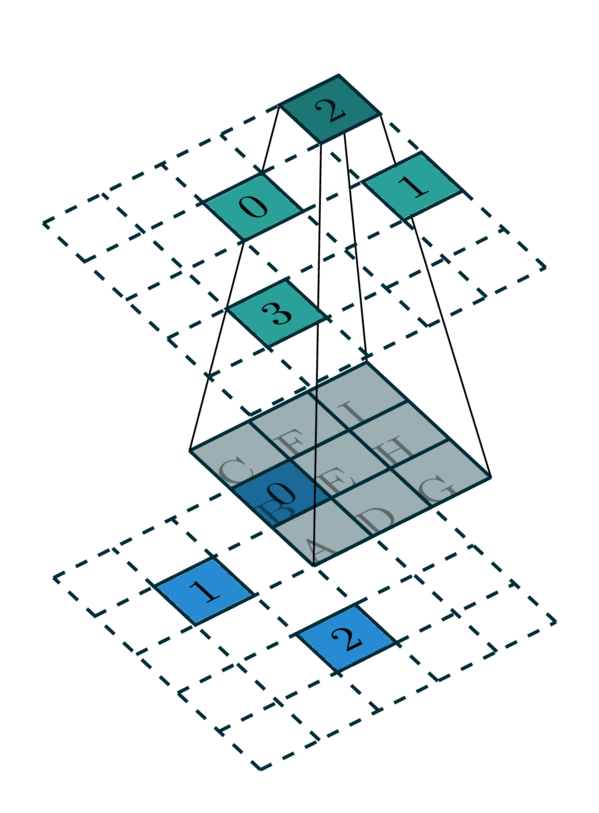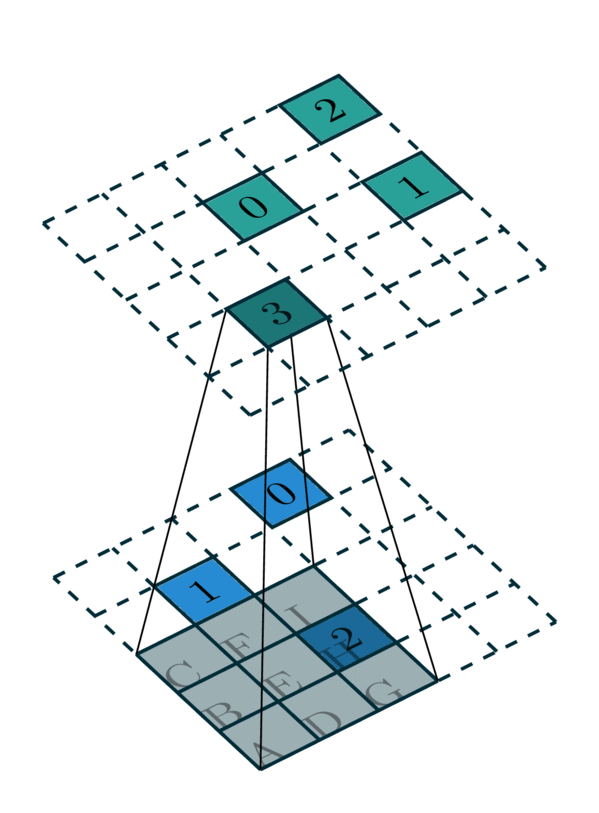
由于单个核映射定义了卷积核的一个特定单元的映射，因此卷积需要多个核映射。 在本例中，对于 \(3 \times 3\) 卷积，我们需要 9 个映射来定义一个完整的核映射。

卷积核映射

kernel_map

[照片来源：Chris Choy]

在此示例中，我们需要所有 \(3\times 3\) 内核的 9 个核映射。 但是，其中一些核映射没有元素。 当卷积核覆盖所有坐标时，我们提取核映射

  • 内核 B：1 → 0

  • 内核 B：0 → 2

  • 内核 H：2 → 3

  • 内核 I：0 → 0